Diagramas de Venn

O lógico do século XIX John Venn criou um sistema de diagramas para representar as informações expressas em proposições categóricas. Esses diagramas ficaram conhecidos como diagramas de Venn. O uso dessa ferramenta é útil para apresentar informações com bastante clareza e assim avaliar uma série de inferências diretas e a validade de silogismos.

Em um diagrama de Venn, são usados círculos para representar cada classe denotada pelos termos de uma proposição.

Os quatro tipos de proposições categóricas são representadas da seguinte maneira.

Todo S é P (A)

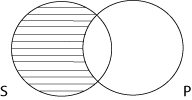
Cada um dos círculos S e P representa um dos termos da proposição “todo S é P”. A área do círculo S que está riscada significa que está vazia, que não há nenhum elemento nessa parte. Todos os membros do conjunto S estão na intersecção entre S e P, já que todo S é também P.

Considere a proposição “todo cachorro tem quatro patas”. O conjunto dos cachorros é representado pelo círculo S e o conjunto dos seres com quatro patas pelo círculo P. Como todos os cachorros têm quatro patas, colocamos todos na parte do diagrama que é S e P ao mesmo tempo.

Nenhum S é P (E)

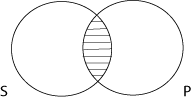
A proposição “nenhum S é P” é representada marcando como vazia a intersecção entre S e P. Com isso se mostra que não existe S que seja ao mesmo tempo P.

Se digo que “nenhum ser humano tem quatro pernas”, S representa a classe dos seres humanos, P a classe dos seres com quatro pernas. No diagrama, não existe nenhum ser humano ou ser de quatro pernas que esteja na intersecção entre S e P. Essa parte dos conjuntos é vazia.

Algum S é P (I)

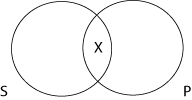
A proposição “algum S é P” é representada com um X na intersecção entre S e P. Com isso se quer dizer que existe pelo menos um elemento de S que também é P. É sempre importante lembrar que, de um ponto de vista lógico, a palavra “algum” significa pelo menos um. Ela não implica que exista mais de um ser, mas que exista pelo menos um.

Se considerarmos a proposição “alguns veículos humanos são capazes de voar”, S representa a classe dos veículos humanos e P a classe dos seres capazes de voar. Do ponto de vista lógico, a frase “alguns veículos humanos são capazes de voar” significa que existe pelo menos um elemento do conjunto S que está presente dentro de P.

Algum S não é P (O)

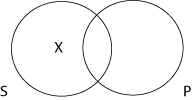
Por fim, a proposição “algum S não é P” é representada com um X na parte de S que não é P. Com isso se afirma que pelo menos um dos elementos do conjunto S não é P e portanto está fora da intersecção entre S e P.

Se afirmo que “algum  animal não sabe voar”, S representa a classe dos animais e P os seres que sabem voar. No diagrama colocamos o animal que não sabe voar fora da intersecção entre S e P para mostrar que esse animal particular não é capaz de voar.

Como avaliar um silogismo

Agora vamos ver como usar esses diagramas para avaliar se um silogismo é válido ou não.

Considere o exemplo abaixo:

Todos os humanos são mortais.

Sócrates é um humano.

Portanto, Sócrates é mortal.

Nesse caso, para a premissa “Todos os humanos são mortais”, podemos representar o conjunto de humanos como um círculo e o conjunto de mortais como outro círculo sobreposto ao primeiro. A sobreposição dos círculos representa o conjunto de humanos mortais. A área do círculo de humanos que está fora da intersecção está vazia, indicando que não existe um ser humano que não seja mortal.

Para representar a premissa “Sócrates é um humano”, podemos incluir um X dentro do círculo que representa o conjunto de humanos. O X representa Sócrates, que é um membro desse conjunto. Como a única área que tem algum ser humano é a intersecção, devemos marcar aí o X. 

Agora podemos ver se a conclusão “Sócrates é mortal” é verdadeira para todos os casos possíveis. Podemos verificar isso no diagrama de Venn, vendo que o X que representa Sócrates está dentro do círculo que representa o conjunto de mortais, tal como afirma a conclusão.

Vamos analisar agora um silogismo com uma premissa particular afirmativa:

Alguns seres humanos são mamíferos.

Sócrates é um ser humano.

Portanto, Sócrates é um mamífero.

Podemos representar as premissas do argumento acima da seguinte forma:

Um círculo com o conjunto de seres humanos que se sobrepõe parcialmente a um círculo com o conjunto de mamíferos, com um X na área de sobreposição para indicar que existe pelo menos um ser humano que é também um mamífero.

Podemos representar Sócrates como um ponto dentro do círculo que representa o conjunto dos seres humanos. E onde colocar esse ponto? Na área de intersecção entre seres humanos e mamíferos ou na área fora dessa intersecção? Como a primeira premissa afirma apenas que “alguns seres humanos são mamíferos”, ficamos com essa dúvida ao representar a segunda premissa e, consequentemente, não temos informações suficientes para dizer que Sócrates é um mamífero. Portanto, o argumento não é válido. As premissas não permitem que cheguemos à conclusão de que “Sócrates é um mamífero”. E podemos observar isso ao construir o diagrama de Venn e ficarmos sem indicação de onde colocar Sócrates, se na área de intersecção ou fora dela.

Por fim, vamos analisar um exemplo de silogismo com uma premissa universal negativa:

Nenhum fluber é friquer.

Todos os quibbles são flubers.

Portanto, nenhum quibble é friquer.

Na premissa 1, marcamos como vazia a intersecção entre flubers e friquers para indicar que não existe nenhum fluber que seja também friquer. Na premissa 2, representamos o conjunto dos quibbles como um terceiro círculo, sobreposto ao círculo dos flubers e com a área sobreposta riscada, indicando que todos os membros do conjunto de quibbles está contida nessa área e a área de quibbles que não são flubers está vazia.

Assim, ao avaliar a conclusão “nenhum quibble é friquer”, podemos verificar no diagrama de Venn que o conjunto dos quibbles está completamente fora da área que representa o conjunto dos friquers, indicando que nenhum quibble é também um friquer. Portanto, a conclusão “nenhum quibble é friquer” é válida.